자료구조란?
- 용어: 자료구조, 데이터구조, data structure
- 대량의 데이터를 효율적으로 관리할 수 있는 데이터의 구조를 의미
- 코드 상에서 효율적으로 데이터를 처리하기 위해, 데이터 특성에 따라, 체계적으로 데이터를 구조화해야 함
- 어떤 데이터 구조를 사용하느냐에 따라, 코드 효율이 달라짐
1. 배열 (Array)
- 데이터를 나열하고, 각 데이터를 인덱스에 대응해주고, 인덱스로 데이터를 접근할 수 있도록 구성된 데이터 구조
- 파이썬에서는 리스트 타입이 배열 기능을 제공하고 있음
배열이 왜 필요한가?
- 같은 종류의 데이터를 효율적으로 관리하기 위해 사용
- 같은 종류의 데이터를 순차적으로 저장
- 배열의 장점:
- 인덱스로 인한 빠른 접근 가능
- 배열의 단점:
- 미리 배열의 크기를 설정해줘야 하므로, 데이터를 추가하는 것이 어렵다
- 데이터를 삭제 할 경우, 뒤에 있는 데이터를 앞으로 당겨와야 하는 어려움이 있다
2. 큐 (Queue)
- 줄을 서는 행위와 유사
- FIFO(First-In, First-Out) 또는 LILO(Last-In, Last-Out) 방식으로 스택과 꺼내는 순서가 반대
기본 용어
- Enqueue: 큐에 데이터를 넣는 기능
- Dequeue: 큐에서 데이터를 꺼내는 기능
3. 스택 (Stack)
- 데이터를 제한적으로 접근할 수 있는 구조
- 한쪽 끝에서만 자료를 넣거나 뺄 수 있는 구조
- 가장 나중에 쌓은 데이터를 가장 먼저 빼낼 수 있는 데이터 구조
스택 구조
- 스택은 LIFO(Last In, Fisrt Out) 또는 FILO(First In, Last Out) 데이터 관리 방식을 따름
- 주요 기능
- push(): 데이터를 스택에 넣기
- pop(): 데이터를 스택에서 꺼내기
스택의 장단점
- 장점
- 구조가 단순해서, 구현이 쉽다
- 데이터 저장/읽기 속도가 빠르다
- 단점
- 데이터 최대 갯수를 미리 정해야 한다
- 저장 공간의 낭비가 발생할 수 있음
- 미리 최대 갯수만큼 저장 공간을 확보해야 함
4. 링크드 리스트 (Linked List)
- 연결 리스트라고도 함
- 배열은 정해진 크기의 공간에 데이터를 나열해야만 하는 단점을 극복한 링크드 리스트는 정해진 크기의 공간 없이, 필요할때마다 데이터를 추가하고 삭제가 가능한 데이터 공간이다. 무한정 크기의 데이터 공간이다
- 배열은 순차적으로 연결된 공간에 데이터를 나열하는 데이터 구조
- 링크드 리스트는 떨어진 곳에 존재하는 데이터를 화살표로 연결해서 관리하는 데이터 구조
기본 용어
- 노드(Node): 데이터 저장 단위 (데이터값, 포인터) 로 구성
- 포인터(pointer): 각 노드 안에서, 다음이나 이전의 노드와의 연결 정보(주소)를 가지고 있는 공간, 다음 노드가 없을 경우 null 값
링크드 리스트의 장단점
- 장점
- 미리 데이터 공간을 미리 할당하지 않아도 됨. 배열은 미리 데이터 공간을 할당 해야 함.
- 단점
- 연결을 위한 별도 데이터 공간이 필요하므로, 저장공간 효율이 높지 않음
- 연결 정보를 찾는 시간이 필요하므로 접근 속도가 느림
- 중간 데이터 삭제시, 앞뒤 데이터의 연결을 재구성해야 하는 부가적인 작업 필요
더블 링크드 리스트
- 이중 연결 리스트라고도 함
- 장점: 양방향으로 연결되어 있어서 노드 탐색이 양쪽으로 모두 가능
5. 해쉬 테이블 (Hash Table)
- 키(Key)에 데이터(Value)를 저장하는 데이터 구조
- Key를 통해 바로 데이터를 받아올 수 있으므로, 검색 속도가 획기적으로 빨라짐
- 파이썬 딕셔너리(Dictionary) 타입이 해쉬 테이블의 예: Key를 가지고 바로 데이터(Value)를 꺼냄
- 보통 배열로 미리 Hash Table 사이즈만큼 생성 후에 사용

기본 용어
- 해쉬(Hash): 임의 값을 고정 길이로 변환하는 것
- 해쉬 테이블(Hash Table): 키 값의 연산에 의해 직접 접근이 가능한 데이터 구조
- 해싱 함수(Hashing Function): Key에 대해 산술 연산을 이용해 데이터 위치를 찾을 수 있는 함수
- 해쉬 값(Hash Value) 또는 해쉬 주소(Hash Address): Key를 해싱 함수로 연산해서, 해쉬 값을 알아내고, 이를 기반으로 해쉬 테이블에서 해당 Key에 대한 데이터 위치를 일관성있게 찾을 수 있음
- 슬롯(Slot): 한 개의 데이터를 저장할 수 있는 공간
장단점과 사용용도
- 장점
- 데이터 저장/읽기 속도가 빠르다. (검색 속도가 빠르다)
- 해쉬는 키에 대한 데이터가 있는지(중복) 확인이 쉬움
- 단점
- 일반적으로 저장공간이 좀더 많이 필요하다.
- 여러 키에 해당하는 주소가 동일할 경우 충돌을 해결하기 위한 별도 자료구조가 필요함
- 사용용도
- 검색이 많이 필요한 경우
- 저장, 삭제, 읽기가 빈번한 경우
- 캐쉬 구현시 (중복 확인이 쉽기 때문)
충돌 해결 알고리즘
해쉬 테이블의 가장 큰 문제는 충돌(Collision)의 경우입니다. 이 문제를 충돌(Collision) 또는 해쉬 충돌(Hash Collision)이라고 부릅니다.
- Chaining 기법
- 개방 해슁 또는 Open Hashing 기법 중 하나: 해쉬 테이블 저장공간 외의 공간을 활용하는 기법
- 충돌이 일어나면, 링크드 리스트라는 자료 구조를 사용해서, 링크드 리스트로 데이터를 추가로 뒤에 연결시켜서 저장하는 기법
- Linear Probing 기법
- 폐쇄 해슁 또는 Close Hashing 기법 중 하나: 해쉬 테이블 저장공간 안에서 충돌 문제를 해결하는 기법
- 충돌이 일어나면, 해당 hash address의 다음 address부터 맨 처음 나오는 빈공간에 저장하는 기법
- 저장공간 활용도를 높이기 위한 기법
빈번한 충돌을 개선하는 기법
해쉬 함수을 재정의 및 해쉬 테이블 저장공간을 확대
시간 복잡도
- 일반적인 경우(Collision이 없는 경우)는 O(1)
- 최악의 경우(Collision이 모두 발생하는 경우)는 O(n)
해쉬 테이블의 경우, 일반적인 경우를 기대하고 만들기 때문에, 시간 복잡도는 O(1) 이라고 말할 수 있음
6. 트리
- 트리: Node와 Branch를 이용해서, 사이클을 이루지 않도록 구성한 데이터 구조
- 실제로 어디에 많이 사용되나?
- 트리 중 이진 트리 (Binary Tree) 형태의 구조로, 탐색(검색) 알고리즘 구현을 위해 많이 사용됨
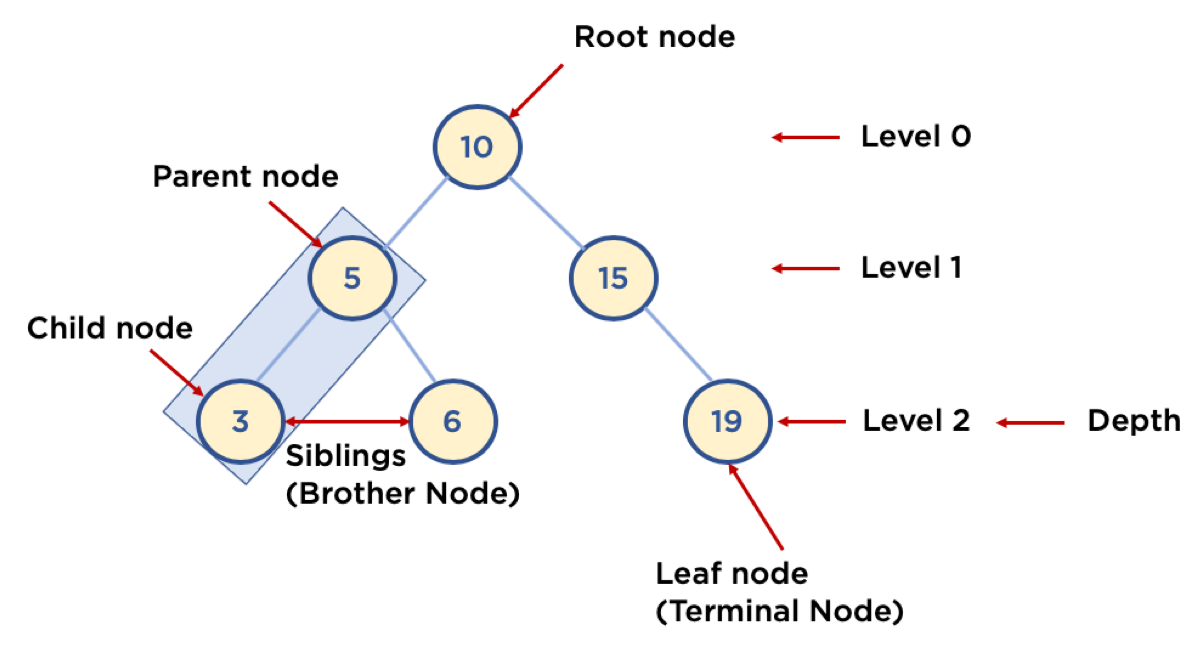
기본 용어
- Node: 트리에서 데이터를 저장하는 기본 요소 (데이터와 다른 연결된 노드에 대한 Branch 정보 포함)
- Root Node: 트리 맨 위에 있는 노드
- Level: 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
- Parent Node: 어떤 노드의 다음 레벨에 연결된 노드
- Child Node: 어떤 노드의 상위 레벨에 연결된 노드
- Leaf Node (Terminal Node): Child Node가 하나도 없는 노드
- Sibling (Brother Node): 동일한 Parent Node를 가진 노드
- Depth: 트리에서 Node가 가질 수 있는 최대 Level
이진트리와 이진탐색트리
- 이진 트리: 노드의 최대 Branch가 2인 트리
- 이진 탐색 트리 (Binary Search Tree, BST): 이진 트리에 다음과 같은 추가적인 조건이 있는 트리
- 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 가지고 있음
이진 탐색 트리의 장점과 주요 용도
- 주요 용도: 데이터 검색(탐색)
- 장점: 탐색 속도를 개선할 수 있음
시간 복잡도
- depth (트리의 높이) 를 h라고 표기한다면, O(h)
- n개의 노드를 가진다면, 에 가까우므로, 시간 복잡도는 𝑂()
- 한번 실행시마다, 50%의 실행할 수도 있는 명령을 제거한다는 의미. 즉 50%의 실행시간을 단축시킬 수 있다는 것을 의미함
이진 탐색 트리의 단점
- 최악의 경우는 링크드 리스트등과 동일한 성능을 보여줌 O(n)

7. 힙
- 힙: 데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)
- 완전 이진 트리: 노드를 삽입할 때 최하단 왼쪽 노드부터 차례대로 삽입하는 트리
힙을 사용하는 이유
- 배열에 데이터를 넣고, 최대값과 최소값을 찾으려면 O(n) 이 걸림
- 이에 반해, 힙에 데이터를 넣고, 최대값과 최소값을 찾으면, 𝑂() 이 걸림
- 우선순위 큐와 같이 최대값 또는 최소값을 빠르게 찾아야 하는 자료구조 및 알고리즘 구현 등에 활용됨
힙의 구조
- 힙은 최대값을 구하기 위한 구조 (최대 힙, Max Heap) 와, 최소값을 구하기 위한 구조 (최소 힙, Min Heap) 로 분류할 수 있음
- 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 같다. (최대 힙의 경우)
- 최소 힙의 경우는 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 작음
- 완전 이진 트리 형태를 가짐
힙과 이진 탐색 트리의 차이점
- 공통점: 힙과 이진 탐색 트리는 모두 이진 트리임
- 차이점:
- 힙은 각 노드의 값이 자식 노드보다 크거나 같음(Max Heap의 경우)
- 이진 탐색 트리는 왼쪽 자식 노드의 값이 가장 작고, 그 다음 부모 노드, 그 다음 오른쪽 자식 노드 값이 가장 큼
- 힙은 이진 탐색 트리의 조건인 자식 노드에서 작은 값은 왼쪽, 큰 값은 오른쪽이라는 조건은 없음
- 힙의 왼쪽 및 오른쪽 자식 노드의 값은 오른쪽이 클 수도 있고, 왼쪽이 클 수도 있음
- 이진 탐색 트리는 탐색을 위한 구조, 힙은 최대/최소값 검색을 위한 구조 중 하나로 이해하면 됨
시간 복잡도
- depth (트리의 높이) 를 h라고 표기한다면,
- n개의 노드를 가지는 heap 에 데이터 삽입 또는 삭제시, 최악의 경우 root 노드에서 leaf 노드까지 비교해야 하므로 에 가까우므로, 시간 복잡도는
- 한번 실행시마다, 50%의 실행할 수도 있는 명령을 제거한다는 의미. 즉 50%의 실행시간을 단축시킬 수 있다는 것을 의미함